Author Archives: Glen Bambrick

Geographic Coordinate Systems

Posted on by
Reply

This blog post has moved to a new home at Final Draft Mapping.

Geographic Coordinate Systems Explained

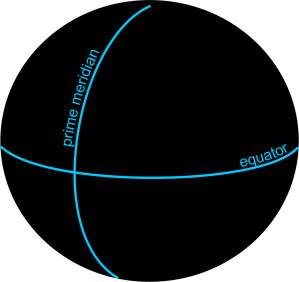
On many occasion I have been handed a file containing geographic coordinates (csv, txt, etc.) to convert to point geometry and view in a GIS and when I plot them they appear anywhere else besides where I expect they should be on the earth. The problem starts with the way the x,y coordinates are perceived. We usually say lat/long coordinates and automatically associate the latitude value with x and the longitude value with y, when in reality it is the other way around. Many GIS software systems ask you to associate a field with the x and y to import data correctly and then you have web mapping like the Google Maps JavaScript API that builds geometry from lat/long which is y,x. It can be a headache getting to grips with geographic coordinates so I hope that this post will go some way to clarifying things to make sure that you embed in your mind that longitude is the x value (think along the equator) and latitude is the y value (think along the prime meridian).

In a geographic coordinate system any location (point) on the earth’s surface can be defined using a set of just two coordinates, a longitude (x-axis) and a latitude (y-axis). Longitude and latitude are angles measured from the equatorial plane and the prime-meridian at the centre of the earth.

I’ll attempt to simplify this in 5 easy steps…

1. Let’s take a model of the earth with the equator and prime meridian defined.

GCS Stage 1

2. Place a point on the surface of the earth and draw a line from the pole to the equator through the point.

GCS Stage 2

3. Draw a line from the closest pole (relative to the point) to the centre of the earth.

GCS Stage 3

4. The longitude coordinate measures the angle between a line drawn from the centre of the earth to the intersection of the prime meridian and the equator (green line) to a line drawn from the centre of the earth to the intersection of the line drawn from the pole, through the point, to the equator (red line).

GCS Stage 4

5. The latitude coordinate measures the angle between the plane of the equator and a line drawn from the centre of the earth to the point (dashed line).

GCS Stage 5

Longitude and latitude coordinates are angles that are generally measured in degrees or radians, but any angular measurement can be used. Degrees, however, are the more commonly used measurement. Longitude values range between -180 degrees (west) and +180 degrees (east) from the prime meridian. Latitude values range between -90 degrees at the South Pole to +90 degrees at the North Pole from the equator.

GCS Degrees

The two most common ways of expressing a geographic coordinate are in degrees-minutes-seconds (dms) and decimal-degrees (dd) formats.

In the dms system each degree is divided into 60 minutes and each minute is divided into 60 seconds. 53° 20’ 52” is an example of a coordinate, but this could be a longitude or a latitude. If we tag an E or W after, then we would know that it is a longitude e.g. 53° 20’ 52” W. Similarly if we tag an N or S after we would know that it is a latitude e.g. 53°20’52” S.

An example of two coordinates representing a location on the surface of the earth is
6° 15″ 34.92′ W 53° 20″ 52.08′ N, which is a point in Dublin, Ireland.

The dd system uses degrees and a decimal fraction of a degree.

An example of two coordinates representing a location on the surface of the earth is -6.2597, 53.3478, which is a point in Dublin, Ireland. So, minus 6.2597 degrees is to the west of the prime meridian and positive 53.3478 is north of the equator. I like to keep longitude as the first coordinate to represent the x value, but I am also aware that the majority use y,x. As such, when using geographic coordinates from a non-spatial file format, it is important to investigate which are the x (long) and y (lat) values especially in cases where header/field information may be missing.

I hope that has gone some way to clarifying geographic coordinates. Check out the posts on using Python to convert decimal-degrees to degrees-minutes-seconds format and also using the Haversine formula to calculate the distance between two sets of coordinates on a sphere.

For further information on Spatial Reference Systems I highly recommend Chapter 1 of Alistair Aitchison’s book ‘Pro Spatial with SQL Server 2012’ published by Apress and available at http://www.apress.com/9781430234913.

Decimal-Degrees (DD) to Degrees-Minutes-Seconds (DMS) with Python

Posted on by
3

This blog post has moved to a new home at Final Draft Mapping

https://learn.finaldraftmapping.com/convert-decimal-degrees-dd-to-degrees-minutes-seconds-dms-with-python/

I am currently transitioning from the comfort of hiding behind buttons and converting to using programming for GIS and geospatial & geostatistical analysis. The code below is an implementation of converting decimal degrees to degrees-minutes-seconds format. The code is heavily commented and hopefully easy to understand.

import math

def dd2dms(longitude, latitude):

    # math.modf() splits whole number and decimal into tuple
    # eg 53.3478 becomes (0.3478, 53)
    split_degx = math.modf(longitude)
    
    # the whole number [index 1] is the degrees
    degrees_x = int(split_degx[1])

    # multiply the decimal part by 60: 0.3478 * 60 = 20.868
    # split the whole number part of the total as the minutes: 20
    # abs() absoulte value - no negative
    minutes_x = abs(int(math.modf(split_degx[0] * 60)[1]))

    # multiply the decimal part of the split above by 60 to get the seconds
    # 0.868 x 60 = 52.08, round excess decimal places to 2 places
    # abs() absoulte value - no negative
    seconds_x = abs(round(math.modf(split_degx[0] * 60)[0] * 60,2))

    # repeat for latitude
    split_degy = math.modf(latitude)
    degrees_y = int(split_degy[1])
    minutes_y = abs(int(math.modf(split_degy[0] * 60)[1]))
    seconds_y = abs(round(math.modf(split_degy[0] * 60)[0] * 60,2))

    # account for E/W & N/S
    if degrees_x < 0:
        EorW = "W"
    else:
        EorW = "E"

    if degrees_y < 0:
        NorS = "S"
    else:
        NorS = "N"

    # abs() remove negative from degrees, was only needed for if-else above
    print "\t" + str(abs(degrees_x)) + u"\u00b0 " + str(minutes_x) + "' " + str(seconds_x) + "\" " + EorW
    print "\t" + str(abs(degrees_y)) + u"\u00b0 " + str(minutes_y) + "' " + str(seconds_y) + "\" " + NorS

# some coords of cities
coords = [["Dublin", -6.2597, 53.3478],["Paris", 2.3508, 48.8567],["Sydney", 151.2094, -33.8650]]

# test dd2dms() 
for city,x,y in coords:
    print city + ":"
    dd2dms(x, y)

The output from running the above script is…

Dublin:
    6° 15' 34.92" W
    53° 20' 52.08" N
Paris:
    2° 21' 2.88" E
    48° 51' 24.12" N
Sydney:
    151° 12' 33.84" E
    33° 51' 54.0" S

I am happy that the output of this script is the same as online converters.